社会ネットワーク（人間同士のつながり）の分析は心理学分野でも数多く行われており，未来の犯罪者を予測したり^[1]，賭博障害からの回復を予測したり^[2]するのに使用されています。ここでは学術社会のネットワーク（論文同士のつながり）を分析することでその分析手法の概観を示します。

使用するデータ

ここでは公開されたCORAというデータを用います^[3]。このデータには2,708本の論文・著書（以下論文とする）とそれらを引用している5,429個のつながりが存在します。また，論文には7つの分野があり，「理論」351本，「強化学習」217本，「遺伝アルゴリズム」418本，「ニューラルネットワーク」818本，「確率的手法」426本，「事例ベース」298本，「ルール学習」180本があります。また，論文全体には1,433個のキーワードがあり，個々の論文にはこれらのキーワードの使用の有無（0と1）を示す1,433個の特徴を示した変数があります。図1はこのデータのネットワークグラフです。同じ形は同じ分野を示すので，同じ分野はお互いに引用しやすく，グループとしてまとまりやすいことがわかります。

べキ分布

社会ネットワークの最大の特徴はベキ分布になる，ということです。図2は論文が引用された数を横軸にとり，該当する論文の頻度を縦軸にとった度数分布です。図2から，多くの論文は2～3回しか引用されない一方，数は少ないものの，20～30回以上引用されている論文や，100回以上という論文もあることがわかります。

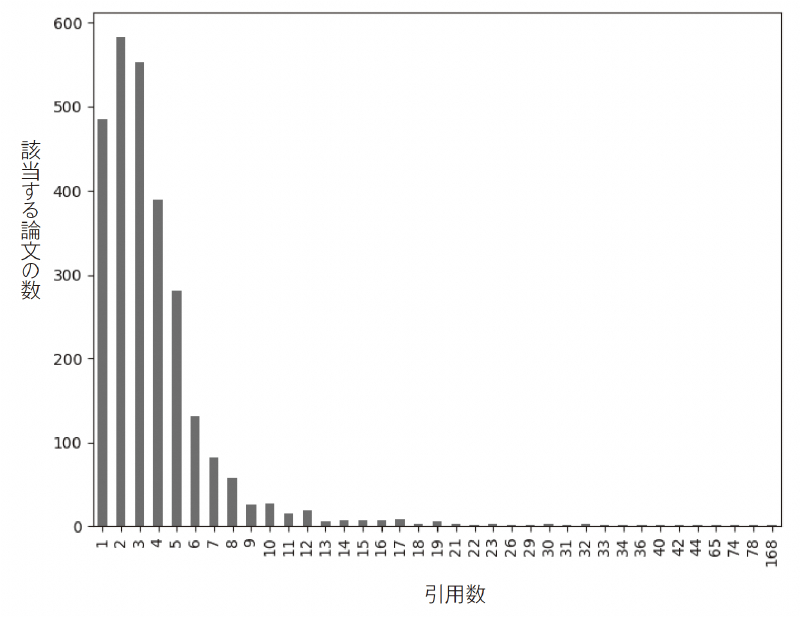
このように最頻値は2～3回であるにもかかわらず，10倍以上や30倍以上のものが存在するような分布をベキ分布といいます。このベキ分布は心理学でよく使用される正規分布とは異なります。正規分布の場合，最頻値が2～3であって，分散が1の場合，4や5の値は存在しますが，20～30の値が存在することはまずありません。

ベキ分布は正規分布と全く違う分布であるため，正規分布を前提にした心理学の検定方法が使えません。この点は社会ネットワークの分析を行う際の最大の注意点です^[4]。

クラスター係数

社会ネットワーク分析ではクラスター係数という指標をよく使用します。これは例えば，自分の友達が10人いたとして，この10人が互いに友達であるかどうかを測る指標です。友達同士が全員友達なら，クラスター係数は1となり，お互いの結びつきが強いグループといえます。一方，友達同士がお互い全く知らなければ，クラスター係数は0となり，結びつきの弱いグループといえます。

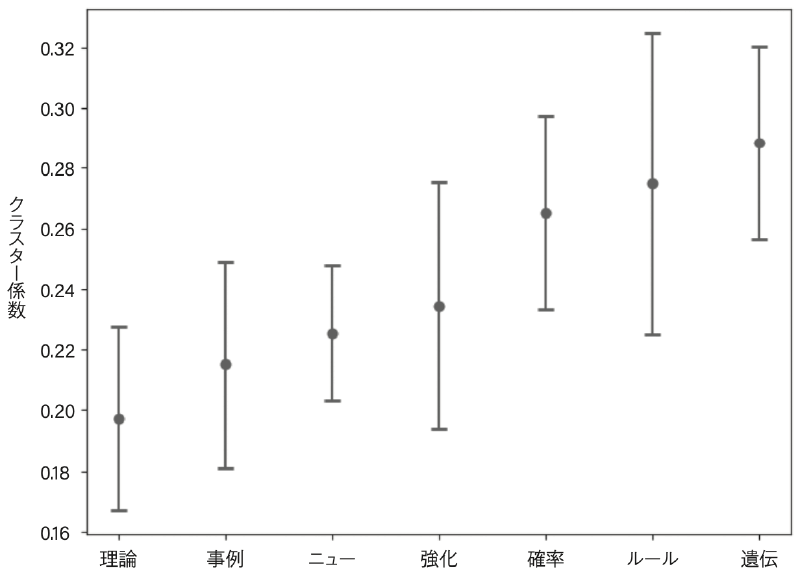
図3に論文の分野ごとのクラスター係数を示します。分野内の結びつきはそれぞれ0.18以上ありますが，「理論」分野が最も結びつきが弱く，「遺伝アルゴリズム」分野が最も結びつきが強いといえます。

グラフニューラルネットワークモデル

心理学では，ある人のラベルを予測することがあります。例えば，その人はたばこを吸うか^[5]，運動するか^[6]などです。 　この予測に際して，その人個人の特徴だけでなく，その人の人間関係も含めたほうが，予測の精度が高くなることが知られています。実際，賭博障害から回復する人は，同じように回復する人同士でつながりを作りやすいことが知られています^[2]。

ここでは，論文の分野をラベルとみなして，その分野を予測します。1つ目のモデルは論文の1,433個の特徴を示した変数から（キーワードが存在するかどうか），その論文の分野を予測します。このモデルを単純モデルといいます。2つ目のモデルは上記の論文の特徴を示した変数に加えて，論文がお互いにどのように引用しあっているかという特徴を示した変数も掛け合わせます。この2つ目のモデルをグラフニューラルネットワークといいます。

データの内の8割はトレーニング用として使用し，残りの2割をテスト用として使用します。トレーニング用データで200回学習し終えた後に，2つのモデルでテスト用データを予測した結果を図4に示します。

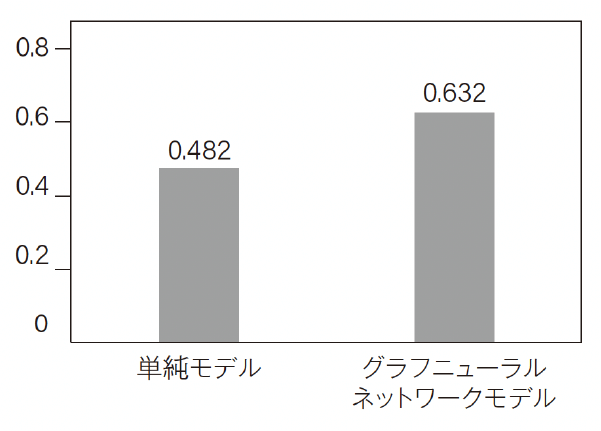
まず，ランダムに分野を予測した場合の正確性（accuracy）は約7分の1（0.14）ですので，このランダムな予測よりも単純モデルとグラフニューラルネットワークの正確性は高いといえます。また，論文同士の引用を入れたグラフニューラルネットワークモデルのほうが，単純モデルよりも正確性が高いこともわかります。

ここから社会ネットワークを組み入れることで，ラベルの予測の正確性が高まったということがいえます。

最後に

社会ネットワーク分析はソーシャルネットワークサービスによって人間関係がデジタルに記録されるようになってから爆発的に飛躍した分野です。公開されたデータが大量にありますので^[7]，ぜひご自身でネットワーク分析を試してみてください。PyTorch Geometric^[8]を使用すればすぐに解析結果を出すことができますので。