時系列で人間を捉える手法

人間は過去から現在，未来へと連続的に続く時間の流れの中で生きているので，人間を理解する最良の方法は，人間の行動とその人を取り巻く環境を長期間にわたってつぶさに観察することです。しかしそれはあまりに高コストで難しいことなので，多くの心理学的研究では，工夫をこらした心理測定尺度や行動指標を駆使して少ない観測時点のデータから人間の行動や心を説明・予測したり，環境との相互作用を明らかにしようとしてきました。

近年では，センシング技術や画像処理技術，IoTの普及に伴って，生態学的妥当性が高いデータを長期間にわたって取得することはさほど困難ではなくなってきています。例えば，手前味噌で恐縮ですが，私の研究1では，ある集落の住民に相互通信するウェアラブル端末を所持してもらい，住民同士の接触を5分間隔で半年間以上にわたって記録しています。そうすることで，その集落の社会的ネットワークを非常に高い解像度で抽出することができました。この例のように長期間にわたり連続的，反復的に観測されたデータは，少数の繰り返し測定しか行わない一般的な縦断データと区別して，強縦断データ（Intensive Longitudinal Data: ILD）と呼ばれ，調査対象者の詳細な時間的な変化だけでなく，人と環境との相互作用に関する情報を提供してくれます。

強縦断データを得るための代表的な手法の一つが，経験サンプリング法（Experience Sampling Method: ESM）です。これは，日常生活を送る調査対象者に対して，何日間かにわたって，一日数回，定刻もしくは無作為な時刻に調査を実施する方法です。経験サンプリングは日誌法に起源を持つ古くからある調査手法ですが，スマートフォンの普及によって格段に手軽に行えるようになりました。

時系列分析の分類

時系列データの分析に必要となるのが時系列分析です。「時系列分析」と呼ばれている手法には，由来する学問分野も考え方も実にさまざまなものがありますが，大まかに分けると以下のような種類があります。

① ARIMA（Auto-Regressive Integrated Moving Average）モデルや潜在成長曲線モデル，中断時系列デザイン，グレンジャー因果性検定など基本的には計量経済学に由来する線形回帰モデル，②隠れマルコフモデルやカルマンフィルターなど，制御理論に由来しベイズ統計と相性が良い状態空間モデル，③ 時系列クラスタリングや関数主成分分析，動的因子分析など多変量解析に由来する分析，④フーリエ変換，ウェーブレット変換，独立成分分析，直交化インパルス応答など信号処理理論に基礎を置く分析，⑤RNN（Recurrent Neural Network）をはじめとする機械学習モデル，⑥再帰定量化分析やCCM（Convergent Cross Mapping）のようにカオスや非線形力学の解析に由来する分析。ここではよく使われる①と②のタイプを紹介します。

線形回帰モデル

このタイプの時系列分析には，時系列の観測値を従属変数とし，別の時系列データの観測値や時間経過自体を独立変数とした回帰分析などが含まれます。

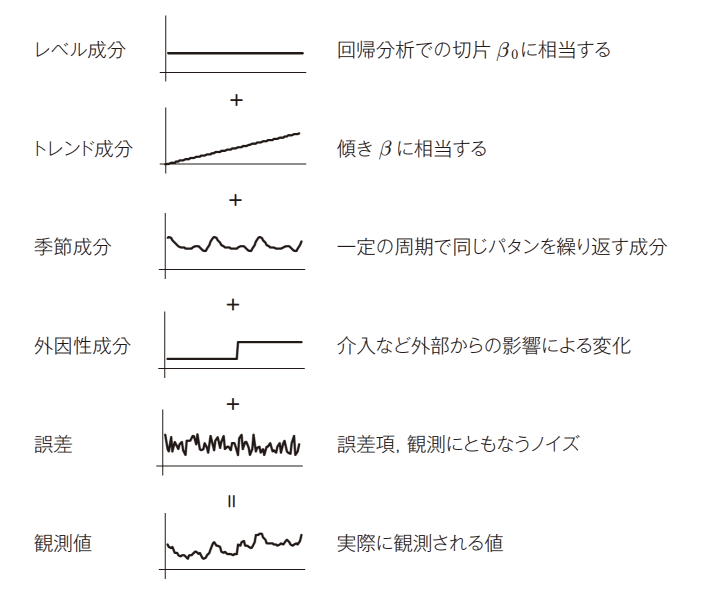
ここでは時系列データをいくつかの要素（成分）が足し合わされたものとして考えます（図1）。レベル成分とは全体を通した平均値です。トレンド成分とはレベルの体系的な変化，つまり長期的な増加もしくは減少の方向性を意味します。季節成分（季節性ともいいます）は，気温が春夏秋冬で変化するように，全体を通して一貫して決まった周期で現れる増加と減少の繰り返しパタンで，その1周期の平均は0になります。外因性成分とは，外部からの影響を表す変数で，計量経済学では外生変数と呼ばれることもあります。さらに偶然によって生じた変化である誤差が加わって観測値となると考えます。

ただ，時系列データの回帰分析には，時系列特有の面倒な点があります。まず，時系列では，2つのデータ系列の間には何も関係がないのに有意な相関があらわれやすいという「見せかけの回帰」と呼ばれる問題があります。「ニコラス・ケイジの年間映画出演本数とその年のプールの溺死者に相関がある」という有名な統計小ネタがありますが，あれこそがまさに「見せかけの回帰」です。この問題を回避するためには，単位根検定や階差系列の作成といった道具立てが必要になります。

また，これとは別に，普通の回帰分析（Ordinary Least Squares: OLS）が適用できない場合があることにも注意が必要です。時系列の場合，ある時点tでの状態はその直前の状態に依存することが多いため，結果的に残差（観測値と予測値の差）に強い系列相関（自己相関）がしばしばあらわれます。そうなると，誤差項に系列相関がないことを前提とするOLSは使えません。そのようなときは，季節成分のモデリングを丁寧に行って残差の系列相関をなくしたり，一般化最小二乗法（GLS）を適用したりする必要があります。

このように，複雑な手続きが必要ではありますが，時系列の回帰分析の考え方を発展させることで，ベクトル自己回帰（VAR）モデルで2つの時系列間の相互影響関係を検証したり，中断時系列デザインによって準実験的に介入の効果を評価したりと，さまざまな研究に活用することができます。

状態空間モデル

時系列データの生成プロセスをより明示的にモデリングする状態空間モデルというアプローチもあります。状態空間モデルとは，心的過程のように直接観測できない潜在的状態の時間発展を記述するモデル（状態モデル）と，その状態を観測する過程に関するモデル（観測モデル）を明確に分離して考える階層モデルです。

ここで，時点tでの状態x_tは，一つ前の時点の状態x_t-₁に依存して定まるとすると，x_tは，1時点前の状態に状態変化のノイズu_t（システムノイズや状態撹乱項と呼ばれます）が加わった値になります。この状態の変化を表すモデルは状態方程式と呼ばれます。

x_t =f (x_t－₁) +u_t（状態モデル）

一方，状態と観測値の関係を表す式は観測方程式と呼ばれます。観測値y_tと状態変数x_tの関係性を表す関数をhとし，観測値に乗るノイズ（観測ノイズや観測撹乱項と呼ばれます）をy_tとすると観測方程式は下のようになります。

y_t =h(x_t)＋v_t（観測モデル）

状態空間モデルの推定には，ベイズ統計などの知識が必要になりますが，パラメータ推定や補間，予測，成分分解などを統一的に扱うことができるという利点があります。また，柔軟なモデリングが可能であることも良い点です。

時系列分析の将来

今後，技術が進歩して，数年，あるいは一生にわたって記録することができるようになったと想像してみましょう。もしかすると，これまで「認知傾向」や「パーソナリティ」といった内的な要因でもっぱら説明されていた個人の行動の多くが，外的な要因や環境との相互作用によって説明できるようになるかもしれません。行動の予測もより正確にできるようになるでしょう。そうなれば，人間の捉え方や理論のあり方も大きく変わるはずです。ここに心理学における時系列データやその分析の大きな可能性があると私は考えています。