- HOME
- 刊行物のご案内
- 心理学ワールド
- 78号 古くて新しい学習心理学
- 学習の理論から強化学習, 計算論モデリングへ
【特集】
学習の理論から強化学習, 計算論モデリングへ

片平健太郎(かたひら けんたろう)
Profile─片平健太郎
2009年,東京大学大学院新領域創成科学研究科博士課程修了。博士(科学)。東京大学進化認知科学研究センター助教,名古屋大学大学院環境学研究科准教授などを経て現職。専門は学習心理学,行動の計算論モデリング。論文はHow hierarchical models improve point estimates of model parameters at the individual level(Journal of Mathematical Psychology)など。
はじめに
ソーンダイクの「効果の法則」。学習心理学を少しでも学んだことのある方にはおなじみの言葉であろう。「結果として満足を伴う反応は,その刺激との結合が強められ繰り返される」,ということなどを述べた法則である。そして,トールマンの「認知地図」,「Rescorla-Wagner モデル」。いずれも学習心理学の教科書に解説されている重要事項であるが,これらは今,学習の基礎理論にとどまらず,最先端のデータ分析や計算論モデリングの基盤となっている。本稿では,具体的な研究事例を紹介しながら,それらの動向について紹介する。
条件づけと強化学習
イヌに「お手」を教えるといったように,動物に新たな行動を獲得させるにはどうすればよいだろうか。人間が「お手本」を見せてそれを真似させようとしても,まずうまくいかない。そこで,エサなどを強化子として動物を目的の行動に近づけていくという,オペラント条件づけの原理が用いられる。では,ロボットに何かの行動をさせるにはどうすればよいだろうか。人間が作るものなのだから,所望の行動をするようにプログラミングすればよい,と思われるかもしれない。しかしこれもなかなか容易ではない。特定の目標物に手を伸ばす運動をさせるだけでも,複数ある関節を連携させるための複雑な計算が必要になる。そんな手間はかけずに,動物のオペラント条件づけのように学習させることができないだろうか。それを実現するのが強化学習である。
強化学習は,行動の良し悪しの評価(報酬)をもとに人工的なエージェントに行動を学習させるための計算手法である。例として,二つのスロットマシンの選択を繰り返す場面を考えよう(図1a)。それぞれのスロットマシンに割り当てられた報酬確率に従い,報酬の有無が決定される。その確率は事前にはわからない。経験をもとにより良い選択肢を選ぶ必要がある。基本的な強化学習モデルでは,各行動により得られる行動価値を計算する。行動iを選択した場合,次のように行動価値の更新を行う(iはスロットマシンAまたはBのいずれかの選択):
動iの価値の変化量=学習率α×(実際に得られた報酬R-現時点での行動iの価値)
つまり,行動iをとって得られた報酬が,その時点での行動iの価値より大きければ,その分,行動iの価値を増加させる。学習率αは0以上1以下の値をとる定数である。この更新式は,冒頭で言及したRescorla-Wagnerモデルの基本形と等価である。行動価値をもとに,選択する行動を決定する。基本的には行動価値の高い行動を選べばよいのだが,価値が高いほうだけを選ぶと,先にたまたま報酬が得られた価値の低い選択肢ばかり選んでしまうかもしれない。より良い選択肢を探索するために,選択はある程度ランダムにしたほうがよい。そこで図1cの関数で計算した確率に従って選択をする。この関数の傾きはパラメータβで決まる。
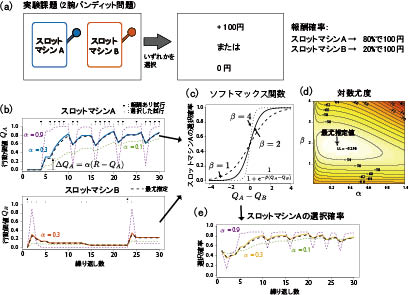
図1 強化学習モデルおよびモデルフィッティングの概要
(a)実験課題の例。この例では,参加者は二つのスロットマシンからの選択を繰り返す。スロットマシンに割り当てられた報酬確率 (右) に従い,報酬の有無が決定される。(b-e)強化学習(α=0.3,β=2.0)によりこの課題を30試行繰り返した例。報酬をもとに行動価値を更新し(b),その行動価値に基づきソフトマックス関数(c)で各選択肢の選択確率を計算する(e)。与えられた行動系列をモデルが生成する確率に対数をとったものが対数尤度である(d)。最尤推定では,この対数尤度を最大化するようなパラメータの組み合わせを推定値として用いる。
データモデリングツールとしての強化学習モデル
強化学習は人工的なエージェントに行動を選択させるための計算手法として研究されてきたものであった。一方,心理学の実験においては,行動選択はヒトやその他の動物が行う。強化学習を行動のモデルと考え,行動データからその内的過程を推定するための分析ツールとして用いることはできないだろうか。そのような発想で,強化学習モデルは行動の分析ツールとして用いられるようになってきた。具体的には,モデルパラメータを選択と報酬の系列データに適合するように推定する。図1dの対数尤度はパラメータを動かしたときの当てはまりの良さを表している。この対数尤度が最も高くなるパラメータ値を用いて,行動価値や選択確率も推定することができる。
行動データからモデルパラメータ推定をすることにどのような意義があるだろうか。その一つとして,行動データから刺激に対する主観的な価値が推定できるということが挙げられる。例えば,Katahira et al.(2011)は選択の結果として情動的な画像を呈示し,ヒトの選択行動データから画像に対する主観的な報酬価値Rを推定している。その結果,快画像は正の報酬価値を持ち,不快画像は負の報酬価値を持つが,その価値の絶対値は快画像より不快画像のほうが大きいという非対称性があることがわかった。つまり,快画像を求めるより不快画像を避けるほうが優先されるということである。主観的価値を選択から推定できる,という特長は特に主観的価値を報告することができない動物研究で発揮される。Mizoguchi et al.(2015)は,覚せい剤依存のモデルラットにおいて,小報酬に比べ大報酬の報酬価値が相対的に大きくなることを報告している。その他にも強化学習モデルのパラメータは個人特性や精神疾患と関連づけられ,それらがどのように行動の背後にある計算過程と対応づけられるかが議論されている。
認知地図とモデルベース強化学習
これまで紹介した強化学習モデルは冒頭で言及した効果の法則を素朴に実装したものといえる。仮に満腹になって食べ物が要らなくなっても,食べ物で強化されてきた行動をとり続けてしまう。一方,実際のヒトやそれ以外の動物は,単にそれまで強化されてきた行動を繰り返すだけでなく,行動の結果得られる報酬や,環境の変化を考慮して行動することもできる。そのような環境の変化や将来起こる事象に基づき選択をする強化学習の枠組みは,モデルベース強化学習と呼ばれている。ここで,モデルとは「こうしたら次はこうなる」という,環境のモデルであり,トールマンの認知地図を一般化したものといえる。
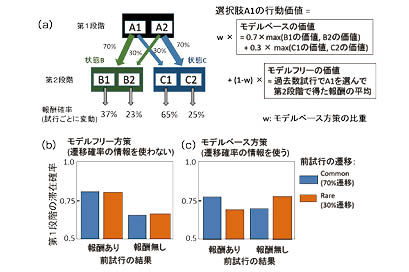
近年ではヒトの行動においてはモデルベースとモデルフリーな方策は共存していると考えられている。そのバランスを個人ごとに計測するために用いられている課題が,図2に示す2段階マルコフ決定課題である(Daw et al., 2011)。この課題は,各試行2回の選択が求められる(図2a)。第1段階の選択に応じた確率で第2段階の状態が決まる(図2a)。例えばA1を選び,稀な遷移(30%)が起きて状態Cに遷移し,C1を選択したとしよう。その後に報酬が得られたので,もう一度状態Cに行きたいとする。その場合,次の試行では前試行と同じA1ではなく,70%で状態Cに遷移するA2を選ぶほうがよい。これが,状態遷移についての「モデル」を利用したモデルベースな方策である。一方,モデルフリーな方策では,A1を選んだあとに報酬が得られたという理由で,もう一度A1を選ぶ。これらの帰着として,図2b, cのような滞在確率のパターンが見られると予想される。成人の健常者はこれらの中間的なパターンが現れる。一方,課題中に認知的負荷をかけた状態や(Otto et al., 2013),衝動性の高い個人においてはモデルフリーの方策の比重が増すことなど(Gillan et al., 2016),方策のバランスと個人特性や状態,発達,精神疾患との関連が明らかにされている。
Daw et al.(2011)が提案したモデルベース強化学習は,将来の状態遷移先の価値の最大値をとり,それに遷移確率で重みをつけて平均をとるという,比較的複雑な計算を要する(図2a右)。これに対し,Toyama et al.(2017)はモデルフリーな強化学習において前試行の遷移情報を使って更新量を修飾するシンプルな計算で,図2cのパターンを説明するモデルを提案した。さらに,そのモデルはDaw et al.(2011)のモデルよりも有意に実際のヒトの選択データに適合していた。データにより適合するモデルが必ずしも真実を反映しているとは限らないが,よりシンプルな原理で,かつ適合性も高いモデルのほうが妥当性は高いといえるだろう。実際にヒトやその他の動物がどのような計算に基づき学習し選択をしているのだろうか。また,どのようなメカニズムで個人特性や状態,精神疾患がその計算原理と関係するのだろうか。さらなる研究が望まれる。
深層学習と強化学習
今,空前の人工知能ブームである。そのきっかけの一つは深層学習(ディープラーニング)の発展にある。深層学習は画像などの高次元情報から学習によりパターンを抽出する方法であるが,それと強化学習を組み合わせ,系列的な行動選択を行う方法が開発されている。Deep Q-Network(DQN)と呼ばれるその手法は,行動価値を深層学習により学習させるものである。DQNは計算機が人間のプロ棋士には勝つことが難しいと考えられていた囲碁でヨーロッパチャンピオンに5戦中5勝し,人々を驚かせた(Silver et al., 2015)。DQNは純粋に計算機に学習をさせるために構築された計算手法であるが,その構成要素は脳の構造を模倣した神経回路モデルと,脳内の計算過程のモデルとして用いられてきた強化学習である。今後,深層学習が心理学に影響を与えることはあるだろうか。逆に,心理学の知見が深層学習の発展に貢献できるだろうか。今後の展開が楽しみである。
展望
学習心理学と最新の神経科学,計算論,人工知能等の諸分野との関係は,依然として混沌としている。それぞれの分野での用語の対応関係は明確ではない。心的過程の構成概念を扱う心理学者としては,それらの概念を吟味し,整理していくことが重要な課題である。一方で,どこまでが学習心理学か,という線引きは難しくなっている。学習心理学自体も計算論や機械学習等の周辺領域の新たな知見を取り入れていくことで,さらに発展していくだろう。
文献
- Daw, N. D., et al.(2011)Model-based influences on humans' choices and striatal prediction errors. Neuron, 69 , 1204-1215.
- Gillan, C. M., et al.(2016)Characterizing a psychiatric symptom dimension related to deficits in goal-directed control. eLife, 5 , e11305.
- Katahira, K., et al.(2011)Decision-Making Based on Emotional Images. Front. Psychol., 2 , 311.
- Mizoguchi, H., et al.(2015)Insular neural system controls decision-making in healthy and methamphetamine-treated rats. Proc. Natl. Acad. Sci. USA, 112 , E3930-E3939.
- Otto, A. R., et al.(2013)Working-memory capacity protects model-based learning from stress. Proc. Natl. Acad. Sci. USA, 110 , 20941-20946.
- Silver, D., et al.(2016)Mastering the game of Go with deep neural networks and tree search. Nature, 529 , 484-489.
- Toyama, A., et al.(2017)A simple computational algorithm of model-based choice preference. Cogn. Affect. Behav. Neurosci ., in press.
PDFをダウンロード
1




